職測數(shù)量關(guān)系:利用定位法巧解概率問題
數(shù)量關(guān)系中的排列組合和概率問題讓很多同學(xué)望而卻步,殊不知里面也有一些題型可以用巧妙的方法解決。今天就帶大家學(xué)習(xí)一種巧解概率問題的方法——定位法。
【例1】某公司的會議室有5排共40個(gè)座位,每排座位數(shù)相同。小王、小強(qiáng)開會時(shí)隨機(jī)入座,則他們坐在同一排的概率是多少?
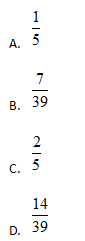
答案:B
解析:

方法二:我們可以發(fā)現(xiàn),小王和小強(qiáng)二人選擇位置是相互聯(lián)系的,也就是一個(gè)人的位置決定另一個(gè)的位置。因此,我們可以先安排一個(gè)人入座,假如先安排小王,他選擇時(shí)每一個(gè)位置均可,因此概率為1;再安排小強(qiáng),因?yàn)樾⊥跻呀?jīng)選擇了一個(gè)位置,可供他選擇的只有剩下的39個(gè)位置,但是要和小王在同一排,因此只能在小王選擇的那一排剩下的7個(gè)位置中選一個(gè),
【小結(jié)】
定位法適用條件:在古典概率問題中,遇到要同時(shí)考慮相互聯(lián)系的兩個(gè)元素。
定位法解題技巧:先將其中一個(gè)元素固定,再考慮其他元素的所有可能情況,從而進(jìn)行求解。
【例2】街道有5個(gè)小區(qū),街道干部小張和民警小王本周各自安排計(jì)劃,在星期一至星期五每天各巡察1個(gè)小區(qū)。如果兩人均是隨機(jī)安排巡查順序,問兩人在本周中至少有3天巡察同一小區(qū)的概率在以下哪個(gè)范圍內(nèi)?
A.低于5%
B.在5%-8%之間
C.在8%-10%之間
D.高于10%
答案:C
【解析】小張和小王在本周中至少有3天巡察同一小區(qū)是相互聯(lián)系的,可以用定位法進(jìn)行計(jì)算。先讓小張安排周一至周五的巡察順序,無任何要求,所以怎么安排都可以。那么小王在安排時(shí),他也可以隨意安排順序,總的等可能樣本數(shù)為 A事件為兩人至少有3天巡察同一小區(qū),分情況討論:①有3天相同:小王先從5天中選擇3天與小張相同,選擇的3天改變順序?qū)Y(jié)果無影響,則有
A事件為兩人至少有3天巡察同一小區(qū),分情況討論:①有3天相同:小王先從5天中選擇3天與小張相同,選擇的3天改變順序?qū)Y(jié)果無影響,則有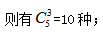 然后再考慮剩下兩天不相同,則只有交換巡察小區(qū)1種方式,分兩步思考因此有10×1=10個(gè)樣本。②有4天相同:因?yàn)?天中要有4天相同,說明剩下1天也兩人也必然相同,因此4天相同與5天相同其實(shí)是一樣的,只能是小王的順序和小張完全一樣,僅有1個(gè)樣本。因此A事件的等可能樣本數(shù)為10+1=11個(gè)。
然后再考慮剩下兩天不相同,則只有交換巡察小區(qū)1種方式,分兩步思考因此有10×1=10個(gè)樣本。②有4天相同:因?yàn)?天中要有4天相同,說明剩下1天也兩人也必然相同,因此4天相同與5天相同其實(shí)是一樣的,只能是小王的順序和小張完全一樣,僅有1個(gè)樣本。因此A事件的等可能樣本數(shù)為10+1=11個(gè)。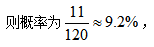 故選C項(xiàng)。
故選C項(xiàng)。







