職測答題技巧：數列構造最值問題的解題思路
最值問題是數量關系中非常重要的一種題型，考察頻率很高。今天 國家事業單位考試網（m.linusblanket.net）與大家探討一下最值問題中常見的構造數列類題型的解題方法。
構造數列類最值問題是最值問題中難度較高的一種題型。主要表現在兩個方面，一是在梳理解題思路中，對各個名次的要求需要分析清楚，是應該盡可能高還是應該盡可能低；二是部分構造數列類最值問題計算難度較高，那么在計算時我們就應該盡量結合一些計算技巧，例如尾數法或者相關公式，以提高計算速度。下面通過幾道例子詳細梳理一下構造類最值問題解題方法的三個步驟如何應用。
構造類最值問題解題方法的三個步驟如何應用
題型特征：最多(少)的…至多(少)…;排名第N的至多(少)……
解題方法：1.排序定位(求誰設誰);2.構造數列(反向推其他);3.加和求解。
例1. 【2014國考】某連鎖企業在10個城市共有100家專賣店，每個城市的專賣店數量都不同。如果專賣店數量排名第5多的城市有12家專賣店，那么專賣店數量排名最后的城市，最多有幾家專賣店：
A. 2
B. 3
C. 4
D. 5
【解題思路】設專賣店數量排名最后的城市有x家專賣店。要求專賣店數量排名最后的城市專賣店的數量最多,則令其他城市專賣店數量最少。題目中已知排名第 5 多城市有 12家專賣店，且每個城市專賣店數量不同,則可得下表:
根據該企業共有100家專賣店的條件，則有16+15+14+13+12+x+4+x+3+x+2+x+1+x=100，解得x=4，正確答案為C。
【點評】本題在解題過程中“構造數列”時，需要注意題干已經給定第五名的城市有12家專賣店，不能忽略掉這一條件，若將第五名構造成“x+5”進行后續計算，結果會出現偏差。提醒大家，在構造數列的過程中，一定要注意題干是否有特定條件。
例2. 【2018國考】某新能源汽車企業計劃在A、B、C、D四個城市建設72個充電站，其中在B市建設的充電站數量占總數的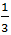
，在C市建設的充電站數量比A市多6個，在D市建設的充電站數量少于其他任一城市。問至少要在C市建設多少個充電站?
A. 20
B. 18
C. 22
D. 21
【解題思路】因為B市建設充電站的數量占總數的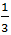，C市又比A市多6個，D市最少，所以四個城市充電站個數關系為：B、C兩市建設充電站的數量較多，A市第三多，D市最少。要使C市建設的充電站盡量少，就要讓其他市建設的充電站盡量多。其中
，
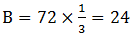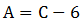，D盡量多且比A少，所以D最多為
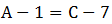。此時充電站總個數
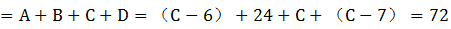，解得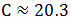
，問至少，應向上取整，所以C至少建設21個充電站。
【點評】在部分構造類最值問題中，解出的答案并非為整數，此時切不可盲目的進行四舍五入，而要根據題目要求進行取舍，提醒大家可以根據口訣進行記憶：“問最多向下取整，問最少向上取整”。例如，我們解出來至多是14.5，那么就不能超過14，此時向下取整，14才是符合要求的答案。
例3.【2010國家】某機關20人參加百分制的普法考試，及格線為60分，20人的平均成績為88分，及格率為95%。所有人得分均為整數，且彼此得分不同。問成績排名第十的人最低考了多少分：
A. 88
B. 89
C. 90
D. 91
【解題思路】
如表所示，設排名第十的人考了x分，要想讓x盡可能低，其他應盡可能高。因每人得分不同，則1-9名最高可為100-92分。同時，不及格人數=20×5%=1人，不及格的人最高只能為59分。11-19名也應盡可能高，設分別比第十名低了1-9分。前9名與倒數第1名的的總分數=96×9+59=923，則第10-19名的總分數=88×20-923=837。即x+(x-1)+…+(x-9)=837，10x-45=837，解得x=88.2分。問最少向上取整，至少為89分，B項滿足。
【點評】此題有兩個特點，第一涉及的名次較多，共有20人，如果20個名次全部構造出來則過于浪費時間，故在解題過程中，分數相連的名次可以列為一格。第二計算量較大，涉及到等差數列的求和以及多位數的加減法。建議考生們在解題過程中一定要掌握相應的計算技巧，在此我們利用等差數列的中位數進行求和便會大大提高我們的計算速度。
例4.【2013國考】某單位2011年招聘了65名畢業生，擬分配到該單位的7個不同部門，假設行政部門分得的畢業生人數比其他部門都多，問行政部門分得的畢業生人數至少為多少名：
A.10
B.11
C.12
D.13
【解題思路】要使行政部門少，則其他部門應盡量多，設行政部門分得x名，其他部門均分得(x-1)名，可列式為x+6(x-1)=65，解得x≈10.1,問最少向上取整，行政部門至少分得11名，正確答案為B。
【點評】在本題中，為什么其他部門分得人數都可以設為(x-1)呢?因為題目中沒有說明“各個部門人數均不相同”。所以提醒大家記住，如果題干沒說均不相等，則可默認相等。
以上就是對于數列構造最值問題的詳細講解。本類題型有一定難度但套路性較強，需要去構造名次及計算復雜方程。在構造名次時，若涉及的名次較少，可以不需畫出表格，而較為復雜的推薦畫出表格，如此解題會更加清晰。提醒大家記住萬變不離其宗，只要知識點掌握牢固、能夠融會貫通，無論如何創新如何結合，我們都可以熟練解決，當然這還需要建立在大量練習的基礎上。
