在考試當中很多時候不是題目不會做，而是時間不夠，尤其是數學部分，一不小心就把自己“套死了”。所以，很多考生都希望擁有能夠把題目“刪繁就簡”，把思路簡單化，把計算過程極簡化的能力。其實，這不是什么超能力，把握好一種思想就可以大大地提高這方面的能力——比例思想。接下來，國家事業單位考試網（m.linusblanket.net）帶大家看看幾道題目，看看比例思想如何賦予你解題“超能力”的。

　　先讓我們一起看看大家談之色變的行程問題。

　　【例1】甲車上午8點從A地出發勻速開往B地，出發30分鐘后乙車從A地出發以甲車2倍的速度前往B地，并在距離B地10千米時追上甲車。如乙車9點10分到達B地，問甲車的速度為多少千米/小時?

　　A.30   B.36   C.45   D.60

　　【解析】A。從有明顯比例關系的地方入手，“乙車從A地出發以甲車2倍的速度”，當乙車追上甲車時，二者走的總路程相同，那么此時乙用的時間為甲的一半。又已知甲“出發30分鐘后”，乙才出發，即乙比甲少用30分鐘，也即從A地到乙追上甲的地點，甲用時60分鐘，乙用時30分鐘。而甲是8點出發的，則乙追上甲為9點。那么最后10千米，乙用時為10分鐘(9點到9點10分)，即乙10分鐘行10千米。乙的速度為甲的2倍，故甲10分鐘可行5千米，一小時(60分鐘)可行30千米，即甲車的速度為30千米/小時。

　　【例2】小張步行從甲單位去乙單位開會，30分鐘后小李發現小張遺漏了一份文件，隨即開車去給小張送文件，小李出發3分鐘后追上小張，此時小張還有1/6的路程未走完，如果小李出發后直接開車到乙單位等小張，需要等幾分鐘?

　　A.6   B.7   C.8   D.9

　　【解析】A。從有明顯比例關系的地方入手，“此時小張還有1/6的路程未走完”，即已經走了5/6的路程。而這5/6的路程里，小張走了30分鐘后小李才出發，也即小李比小張少用30分鐘。那么從小李追上小張處出發，余下1/6的路程，小李比小張少用6分鐘，也即如果小李出發后直接開車到乙單位等小張，需要等6分鐘。

　　然后是資料分析。由于比例思想學習主要是在數量關系部分，所以很多考生也只在數量關系部分可能會考慮比例法。但是作為一種數學思想，比例法是可以運用到所有符合其運用特征的環境里的。資料分析本質上也是數學題目，其中很多描述具有明顯的乘除特征，在這些題目里，其實比例法也是可以運用的。如果運用得當，必然會讓你事半功倍，如魚得水。

　　【例3】2016年我國東部地區研發經費為10689.4億元，首次邁上萬億臺階;比上年增長11%，占全社會研發經費的比重為68.2%，比上年增加0.2個百分點;中部、西部和東北地區研發經費支出分別為2378.1億元、1944.3億元和664.9億元，分別比上年增長10.8%、12.3%和0.4%，所占比重分別為15.2%、12.4%和4.2%。

　　問題：若各地區保持2016年研發經費增長速度不變，2017年西部地區研發經費占全社會的比重為( )。

　　A.12%   B.12.4%   C.12.6%   D.13%

　　【解析】C。將研發經費最小的東北地區的經費支出看成1份，那么，東部、中部和西部，分別對應約為16、4、3份。各地區保持2016年研發經費增長速度，則2017年東北地區、東部、中部和西部分別約為1.004、17.76、4.32、3.369份，其中西部地區研發經費占全社會比重約為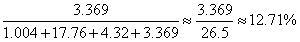，選擇最接近的C。