特值法作為一種解題思想、一種方法在行測的數量關系解題過程中有著重要的作用，學好特值法能夠很好的解決如：利潤、行程、工程等相應的問題，將會大大提升解題的速度及正確率。但是就現在看來，不少同學對于什么時候該用特值、怎么用特值并不是很清楚，所以現在就將相關的思路與大家交流，主要從什么是特值?核心是什么?什么情況可以設特值?怎么設?四個方面來探討，以此來強化這一塊內容的學習!

 

 

 

 

　　簡單的講特值就是講題目中的未知量設為特殊值，從而簡化運算的一種方法?

 

 

　　Eg：張三去買蘋果，買3元/千克的蘋果花了一半的錢，剩下的錢買了2元/千克的，那么兩種蘋果的平均價格是多少?

 

 

　　分析：想要知道蘋果的平均價格就得知道張三有多少錢，以及買了多少千克的蘋果，但是這是未知的。其實不管張三有多少錢，兩種蘋果的單價是固定不變的，而平均價格同樣是不變的。那么不妨設張三有6元錢，一半的錢即有3元買了3元/千克的可以買1千克;余下的3元買2元/千克的課買1.5千克，所以6元錢一共買了2.5千克的蘋果，均價為6÷2.5=2.4元/千克。這就是特值，將未知量設為特殊值從而簡化了運算。

 

 

 

 

　　核心可以簡單理解為：不設未知數，而設“1”(“1”可以是真正意義的1，也可以是方便計算的數)正如上題，我們將特值設為了6一樣。

 

 

 

 

　　1、含有“任意”性描述可考慮使用特值。

 

 

　　Eg，任取一個數，相繼依次寫下它所含的偶數個數、奇數個數與這兩個數字之和，得到一個新的正整數，在寫下這個新的數的偶數、奇數個數與和，又將得到另一個數，如此進行，最后的運算結果是?

 

 

　　A,11 B,111 C,121 D,123

 

 

　　分析：題目求任取一個數，那么可以隨意取，但是為了方便計算，最好取得簡單：如取12，偶數個數為1，奇數個數為1，和為2，組合得到112;在寫112這個數，偶數個數為1奇數個數為2，和為3，組合達到123,;在寫123，偶數個數為1，奇數個數為2，和為3，組合得到123······由此最后的結果無論如何都是123，選擇D項。

 

 

　　2、出現比例百分數計算關系時也可考慮使用特值。

 

 

　　Eg.一批零件需要增加工人，其中占工人總是40%的第一道工序要增加20%的人;占工人總是30%的第二道工序需要增加30%的人，占工人總是20%的第三道工序需要增加40%的人。如果將工人工資總支出的漲幅控制在20%，那么這些工人的平均工資將：

 

 

　　A,下降8% B,上漲8% C,下降4% D,上漲4%

 

 

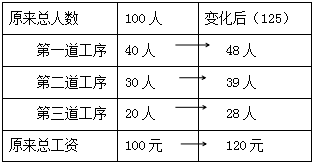
　　分析：由于題目中只有相對于的百分數，原來工人的總數不知道，原來的總工資也不知道，如果知道原來總人數、原來總工資，題目也就變得簡單。不妨設原來總人數為100人，總工資也為100，平均工資為100÷100=1元。變化后如表

 

 

　　由表，工人現在平均工資為120÷125=0.96，下降4%。選擇C項。

 

 

　　1、題目中所求為乘除關系(即M=A×B)，且對應量未知時也可考慮特值。

 

 

　　Eg，甲乙丙三個工程隊，工作效率之比為3：4：5。甲單獨完成A工程需要25天，丙單獨完成B工程需要9天。若三隊合作完成這兩項工程需要多少天?

 

 

　　分析：要求三隊合作多少天，求時間，而相對應的工作效率不知，工作總量也未知，可以考慮特值。題目給出三隊的效率比，不妨設甲乙丙的效率為3、4、5。那么A的工作總量為3×25=75，B的工作總量為5×9=45，AB總量為75+45=120 那么合作時間為120÷(3+4+5)=10天。

 

 

　　通過上述的簡單講解我們已經知道在什么題型特征的情況下可以用特值，由此我們也可以總結一些設特值的簡單方法：

 

 

　　(1)、題目 中有任意描述時：如任意一個數、任意四邊形時，盡量設小、設整以方便計算;而幾何問題通常設特殊四邊形或特殊點;

 

 

　　(2)、題目中出現比例關系時，通常是最簡比為特值;

 

 

　　(3)、題目中涉及濃度、利潤常設整十、整百以方便計算

 

 

　　(4)、在M=A×B關系中，如工程問題條件給出時間時，常設不變量為時間的最小公倍數。